Today I made the final cut to the desktop so the rack will now fit. As seen in earlier photos of this project, the two sides of the desktop met in the corner at a 45 degree angle miter joint. As it turned out, another ham with an Isosceles Triangle Calculator came to my rescue.
One Chance To Get It Right
To fit the radio rack into the corner of the room, I needed to figure out how much to cut off of the right side of the desktop in order to fit a 22″ wide rack in between the two 45 degree angled sides. The desktop currently occupies the entire length of the wall, and shortening its length is now the only solution.
I’m no math whiz, and my guess was I would have to cut off 11″ if I were to fit a 22″ wide rack in between the two sides. Wrong! Luckily, I asked around first. The answer was found using an Isosceles Triangle calculator.
The Isosceles Triangle Calculator
All I knew was the corner was 90 degrees and the hypotenuse was 22″. Thanks to Cory AE6GW for doing the math. The resulting calculation showed I needed to reduce the length of the desktop by 15.556″ in order to obtain an exact fit. Then, I added an inch, so my sliding closet door would still have clearance.
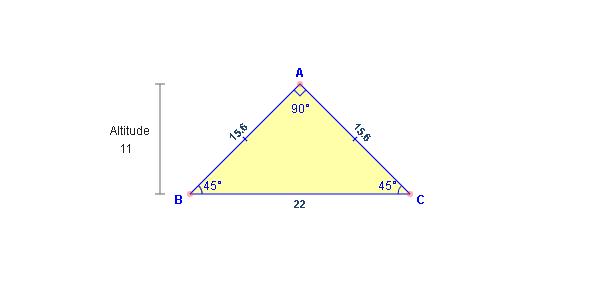
Solving an isosceles triangle. The base, leg or altitude of an isosceles triangle can be found if you know the other two. A perpendicular bisector of the base forms an altitude of the triangle. This forms two congruent right triangles that can be solved using Pythagoras’ Theorem. (It’s all Greek to me)

The right side of the desktop is now approx 16.5″ shorter, and of course the rack now fits squarely into the corner of the room. Exactly the way I wanted it. I say approximately due to the accuracy of the “Armstrong Saw” I used to make the cut!
Although still far from being finished, at least now I can push the rack back into the corner and make a little more room to move around in here.